OVERVIEW
A preliminary simulation exploring the more advanced features of SRIM 2013/TRIM with custom input files, and observing the effects of various ion energy distributions on sputtering, implantation, and target damage with randomized ion angles is detailed. Three different ion energy spread distributions using Nitrogen impinging upon a stainless steel target surface are input and simulated. For standard simulations, TRIM simulates the interactions between the impinging ions upon a selected target. However, the default mode only accounts for ions at a single energy in an ion beam, with only a single angle of incidence to the target, with positions randomly varied across the surface over +/-1 atomic diameter. In order to better simulate cases such as a diffuse glow discharge plasma, a custom input file needs to be generated to vary ion energies and angles over a wider surface area. A custom Python script was written to generate the necessary .DAT input file with appropriate file configuration to the TRIM software based on user inputs. Ion atomic number, ion energy, ion starting position, and impinging angle can be varied based on user inputs. For each simulation, a set of 9999 ions were flown with a variety of random distributions for various parameters. An atomic number of 7 for Nitrogen was selected. Starting position at the surface was selected, as well as randomly varied with a uniform distribution between -100 and +100 angstroms, as opposed to the standard TRIM random lateral variation of +/- one atomic diameter. The impinging ion angles upon the surface were given a uniform random distribution between 0 and 1 for Cos(x), indicating all ions traveling towards the surface of the target, -1 and 1 for Cos(y) and Cos(z), indicating various angles incident to the surface with a value of Cos(0) indicating normal to the surface at the appropriate angle. For ion energy, a maximum energy of 500eV was selected. Three different distributions are compared over varying ranges:
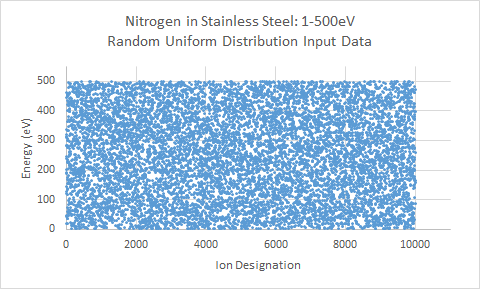
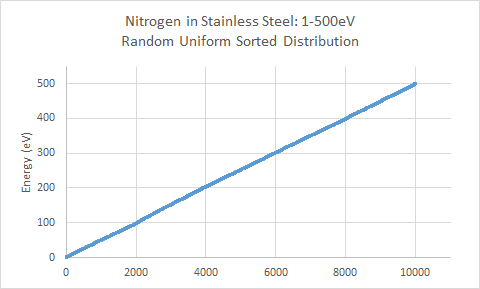
1.) Uniform Random Distribution from 1eV to 500eV
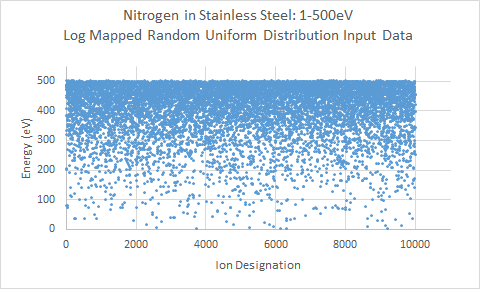
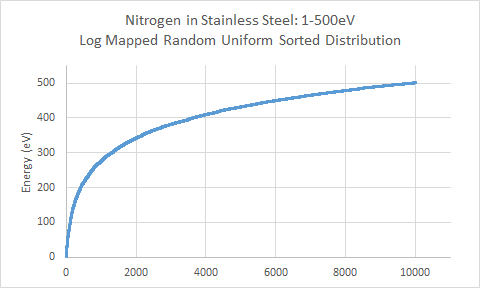
2.) Uniform Random Distribution Mapped to a Logarithmic Curve from 1eV to 500eV
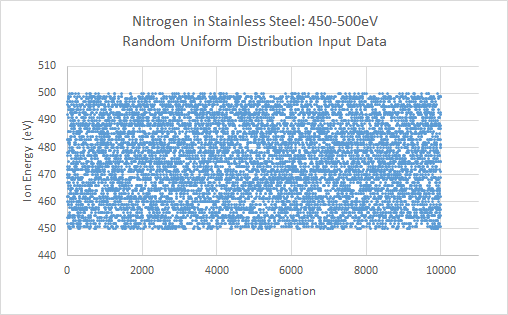
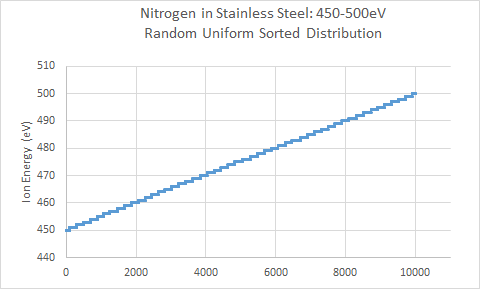
3.) Uniform Random Distribution from 450eV to 500eV
A default stainless steel composition from the program consisting of 8% Chromium, 74% Iron, and 18% Nickel, with a total average density of 8 g/cm^3 was selected as the target. A depth of 60 angstroms was selected to show the lowest full ion travel in the material without passage of any ions through the selected layer width.
These results explore the use of custom .DAT input files and how surface effects vary as a result of randomized input angles and energies.
DATA
I. RANDOM NUMBER DISTRIBUTION INPUTS FOR ION ENERGY
II. ION DEPTHS INTO TARGET
III. ION RANGES/CONCENTRATIONS IN TARGET
IV. 3D ION DISTRIBUTIONS IN TARGET
V. TARGET SPUTTERING
VI. COLLISION EVENTS
VII. RECOIL DISTRIBUTIONS
VIII. ENERGY LOST TO RECOILS
IX. ENERGY LOST TO IONIZATION (ELECTRONS)
X. ENERGY LOST TO PHONONS
RESULTS AND DISCUSSION
I. RANDOM NUMBER DISTRIBUTION INPUTS FOR ION ENERGY
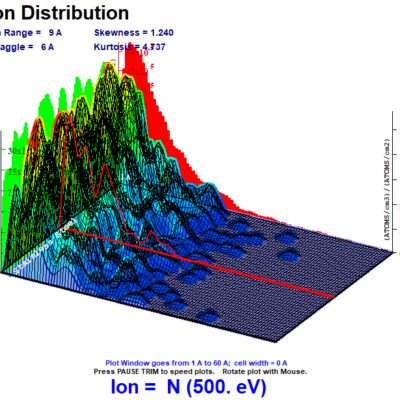
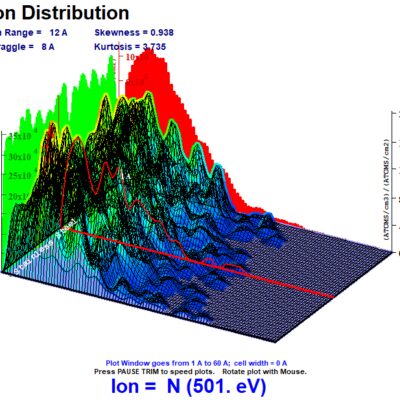
The above graphs illustrate the major data plots generated by TRIM for the various energy distributions for Nitrogen on stainless steel. Section I of the above data shows the energy distribution for each of the three cases. The first and third cases are random uniform distributions between the set min and max energies for the simulation. The second case takes a random uniform distribution and maps the data to a logarithmic curve. This is used to create an ion distribution that has a higher weight and percentage of ions in the upper ion energy, with a rapidly decreasing tail at lower energies. The first case presents the most unrealistic input of ion energy distributions in the plasma. Although various energies will be seen from impinging ions, ion energies will not be expected to be uniformly distributed between ground potential and the upper applied potential, in this case, of 500V. However, it was included to compare the effects of simulation results, particularly with sputtering, from the other two cases, to give an estimated lower bound of sputtering and target damage. The third case utilizes a random uniform distribution between 450-500eV, for an upper bound of energies concentrated within 50eV of the maximum energy. The second case utilizing the log-mapped distribution presents an intermediate energy distribution between the first and third cases, where the bulk of ion energy is at the upper potential limit, and fewer ions at the lower potential limit. In this case, about 50% of the impinging ions are between 450eV and 500eV. About 30% of the ions are between 300eV and 450eV, and the remaining 20% of ions are between 1eV and 300eV.
II. ION DEPTHS INTO TARGET
Section II looks at the depths of the impinging ions from 1-60 angstroms. In all cases, no ions penetrated into the stainless steel layer more than 51 angstroms deep. As expected, the bulk density range of ions increases from Case 1 to Case 3.
III. ION RANGES/CONCENTRATIONS IN TARGET
Section III further elaborates on the data from Section II by providing a graph detailing the concentration of ions at a given depth. In order to obtain actual ion concentrations, or ion density distribution, the y-axis units of (Atoms/cm^3)/(Atoms/cm^2) must be multiplied by the dose (Atoms/cm^2) to obtain the density distribution (Atoms/cm^3). This number is important to determine implantation and loading effects of the surface material, which can greatly vary between different gases when all other parameters are equal. This is further explored in the next study that will compare the effects of different gases on sputtering and surface loading from glow discharge cleaning. Based on the results and energy distributions, it can be seen that for Case 1, a peak concentration is found at a much shallower depth than Cases 2 and 3, which have a much larger proportion of higher energy ions. Cases 2 and 3 exhibit more similar distributions than Case 1, as the bulk majority of ions are at the upper energy limit for Case 2 than Case 1.
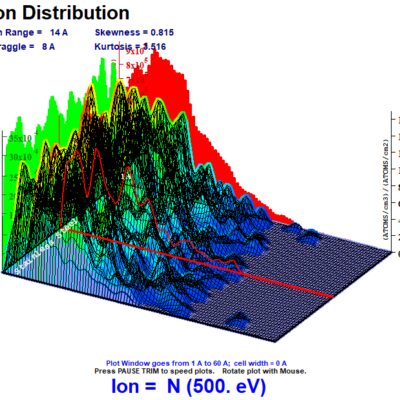
IV. 3D ION DISTRIBUTIONS IN TARGET
Section IV plots the Section III distribution over a 3D graph. The data is smoothed from the original raw data. This is plotted from Section III data to show the ion distribution in the target at various depths across the surface of the target. This is dependent on the energy and incident angle for each randomly generated ion flown into the target at the randomly distributed positions across the surface, over a width of 200 angstroms.
V. TARGET SPUTTERING
Section V details sputtering as a result of each of the energy distributions. As expected, sputtering yield increases from Case 1 to Case 3. However, sputtering yields are shown to be half as much for the Case 1 distribution vs. Cases 2 and 3, where Cases 2 and 3 show very similar sputtering yields, despite the fact that Case 2 has 50% of its ions with the same energy range as Case 3. In all cases, incident ion angles are even distributed with a uniform random function. The following numbers are presented for each of the three cases:
CASE 1: UNIFORM EVEN DISTRIBUTION 1-500eV
i.) Total Sputtering Yield – 0.7750 atoms/ion
ii.) Chromium sputtering Yield – 0.0679 atoms/ion
iii.) Iron Sputtering Yield – 0.5764 atoms/ion
iv.) Nickel Sputtering Yield – 0.1312 atoms/ion
CASE 2: LOGARITHMIC MAPPED UNIFORM EVEN DISTRIBUTION 1-500eV
i.) Total Sputtering Yield – 1.2450 atoms/ion
ii.) Chromium sputtering Yield – 0.1034 atoms/ion
iii.) Iron Sputtering Yield – 0.9269 atoms/ion
iv.) Nickel Sputtering Yield – 0.2143 atoms/ion
CASE 3: UNIFORM EVEN DISTRIBUTION 450-500eV
i.) Total Sputtering Yield – 1.4140 atoms/ion
ii.) Chromium sputtering Yield – 0.1215 atoms/ion
iii.) Iron Sputtering Yield – 1.0500 atoms/ion
iv.) Nickel Sputtering Yield – 0.2469 atoms/ion
Despite having a concentration of 50% ions at energies lower than 450eV, Case 2 yields are nearly the same as Case 3 yields. This implies the significance of sputtering yield of higher energy ions vs lower energy ions. As an important side note, sputtering yields are dictated by the Surface Binding Energy (SBE) of the target atoms. These numbers are very difficult to know and predict, and can vary widely based on a variety of surface conditions. Therefore, the default SBE of 4.3eV is selected to compare relative sputter yields for all target atoms in each case.
VI. COLLISION EVENTS
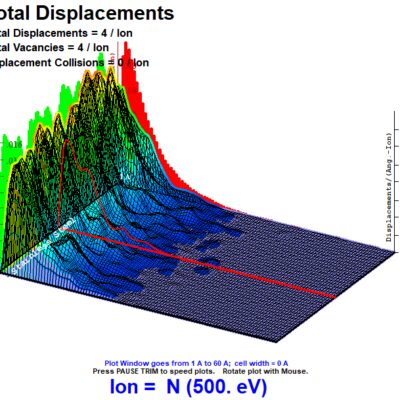
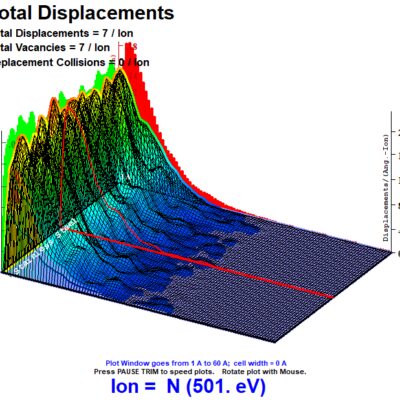
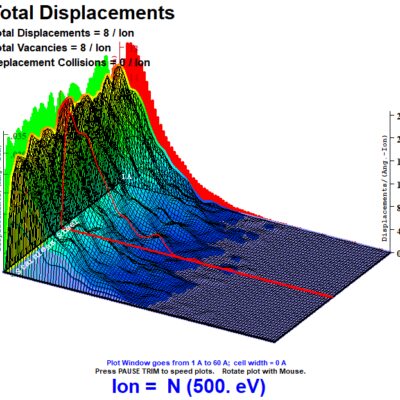
Section VI looks at collision events in terms of depth (angstroms) vs collisions (number/angstrom-ion). This shows total displacements made by the incoming ion as well as associated recoiling target ions. Case 1 ends up with twice as few resulting collision events at 4 target displacements/ion from Case 3 at 8 target displacements/ion, with Case 2 again being nearly similar to Case 3 at 7 target displacements per ion. Peak collision events occur at a depth of around 12 angstroms for all three cases, with a larger tail of collisions occurring deeper in the target for Cases 2 and 3 due to the higher proportion of high-energy ions. Total displacements are further graphed across a 3D plot, which shows the distribution of collision events across the width of the simulated surface, over a length of 200 angstroms. As can be seen from the plots, the Cases 2 and 3 have more displacements deeper in the stainless steel target due to the higher number of higher energy ions in the distribution than Case 1, with Case 3 having slightly more displacements deeper in the target than Case 2.
VII. RECOIL DISTRIBUTIONS
Section VII details recoil distributions. This shows the energy absorbed from each incident ion based on target element composition. As expected, iron, having the highest concentration in the stainless steel, absorbs most of the incoming ion energy from recoils. Both Cases 2 and 3 have a wider trailing distribution in the deeper angstrom regions than Case 1, which is similarly seen in the Section IV collision event plots.
VIII. ENERGY LOST TO RECOILS
Section VIII details energy loss of incoming ions due to recoils. This looks at which elements in the stainless steel composition absorbs the most energy from the impinging Nitrogen ions. Due to its highest molecular mass, Nickel contributes a larger amount of energy loss compared to Iron and Chromium per incident Nitrogen ion. Here, we can see that for Case 1, each ion loses about 17eV/angtrom-ion, where Case 2 loses 25eV/angstrom-ion, and Case 3 loses about 28eV/angtrom-ion for Nitrogen-Nickel interactions.
IX. ENERGY LOST TO IONIZATION (ELECTRONS)
Section IX details the electronic energy losses of the ions, or the losses of the ions due to target electrons, in terms of eV/angstrom. The red plot of the chart details losses from target ion electrons. These losses increase from Cases 1 to 3, at 10eV/angstrom, 12eV/angstrom, and 14eV/angstrom respectively. The blue plot details the electronic losses from recoiling target atoms. Since recoiling atoms are considerably slower than the relative motion of target electrons, the total interactions are less for these losses. Despite this, at the peak of ionization losses for all three cases, losses due to target electrons and recoiling electrons are almost the same, with Case 1 having fewer losses due to recoiling atoms than target electrons.
X. ENERGY LOST TO PHONONS
Section X details the energy loss and phonon generation from impinging Nitrogen ions due to phonons in the target material. Phonons are described as a bulk oscillation or vibration of a lattice of atoms or molecules. For a given interaction, if the transferred energy is less than the displacement energy, or the minimum energy required to knock a target atom out of its lattice site far enough away from it to not immediately return to its original position, then it will return to its original site and release recoil energy which is transferred to a phonon. In all three cases, the vast bulk of phonons are generated from recoiling atoms vs. phonons produced directly from the impinging Nitrogen ions. However, for Cases 2 and 3, the peak phonon generation is due to recoiling atoms over ion interactions, whereas Case 1 shows a peak generation of phonons due to direct ion interactions greater than recoiling atoms at the surface of the stainless steel. For all three cases, the peak phonon generation due to recoils falls in the region of slightly less than 10 angstroms, with Cases 2 and 3 having similar distributions and much higher phonon generation than Case 1.
CONCLUSION
A study comparing the effects of 3 different energy distributions for Nitrogen ions impinging on stainless steel are presented using SRIM/TRIM, as well as a custom Python script to generate the properly formatted input data file. While it was expected that sputtering yields, implantation, and target damage would increase from Cases 1 to 3, it was unexpected that Cases 2 and 3 would yield such similar results for all interactions studied. Case 1 represents the lowest bound, of resulting sputtering yield and target damage, with a uniform random distribution from 1eV to 500eV. Case 2 represents a uniform random distribution of ion energies mapped logarithmic from 1eV to 500eV, while Case 3 represents a uniform random distribution of ion energies from 450eV to 500eV.
For a glow discharge plasma, various interactions between the ions and background gas, as well as ion-ion interactions, system geometry, and fluctuations in the power supply can greatly affect these resulting final ion energy upon the target surface. The above cases represent unrealistic scenarios for angular and energy distributions, which greatly differ from actual angular and energy distributions reported in literature. This study was used primarily to look at varying the inputs to TRIM using a custom input file and observing the outputs. Actual DC glow discharge plasmas with proper distributions will be presented in subsequent simulations utilizing the same Python code, modified to include appropriate distributions, to generate realistic data for simulating such glow discharge plasmas.