TOTAL GAS LOAD DUE TO OUTGASSING AND DETERMINATION OF ULTIMATE PRESSURE
SYSTEM DESIGN V4
Now that molecular and transitional flows for various process gases have been calculated for the current system, the total outgassing load for the system during pumpdown can be found, ultimately leading to the final estimate for the ultimate vacuum attainable for a variety of pumpdown conditions. This section is perhaps one of the most important and powerful of the sections so far, and can give one a very good idea of what vacuum levels they can expect based on their system design. This is notably most important for pumping down the system, as well as knowing the upper and lower bounds for gas loads supported by the system. The following includes the PDF for the entire process for system V4:
The following sections break down and explain each section of the PDF calculations:
1.) Determination that the Selected Pump is Appropriately Sized for the System
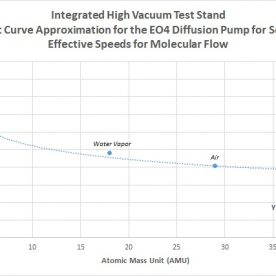
As a general rule of thumb for designing high vacuum systems, the maximum speed of the pump should be at least two times or greater than the effective speed found for the system. This is calculated for both molecular and transitional flows. For molecular flow, the speed of the pump is 600 L/s for air (800 L/s for hydrogen). The effective speed was calculated to be 17.043 L/s for water vapor (since we are focusing on pumpdown for these calculations), in which case the speed of the pump is significantly higher than twice the effective speed for molecular flow. Therefore the pump selected is well suited for the system in terms of speed. For transitional flow, based on the pressure vs. speed curve, at the calculated level of 10^-2 Torr, the maximum speed, for air and other equivalent molecular weight gases, is around 100 L/s. The effective speed at this level for water vapor at 10^-2 Torr was found to be 19.100 L/s. Therefore, the pump is also well sized for the system for transitional flows as well.
If we want to double-check for other gases, we can look at the worst case scenario, which would be deuterium. For molecular flow, the effective speed is 49.241 L/s, which falls well below 800 L/s for the pump. The effective speed for transitional flow is 42.265 L/s (assuming a max pumping speed of 100 L/s @ 10^-2 Torr for hydrogen), which is also within the acceptable rule of thumb speed parameter. Therefore the pump should be able to handle any other gas since hydrogen/deuterium is the most demanding for this criteria.
2.) Maximum Theoretical Gas Loads for Ultimate Operating Pressures at Various Flows
A second general rule of thumb design criteria for designing high vacuum systems is that the system should be capable of reaching at least 1/10th the working pressure. That means that the ultimate pressure attainable should be at least 10 times lower than the desired process working pressure. This is very easy to calculate out and is presented in the PDF. For a working pressure of 1x10^-7 Torr for example, the ultimate pressure attainable of the system should be 1×10^-8 Torr. Therefore the ideal minimum ratio is: P(ultimate)=1/P(working).
Since we roughly know the ultimate pressures needed (in the case of this system, the lowest vacuum required would be around 10^-8 Torr), we can calculate the maximum allowable gas load for the system for both molecular and transitional flows. From the equation S=q/P, solving for q, or gas load, we get q=SxP, where S is the effective speed and P is the ultimate pressure. Since pumpdown pressures are being solved for, the effective speed of 17.043 L/s for molecular flow, and 19.100 L/s for transitional flow average value for transitional flow, (assuming operations at 10^-2 Torr), for water vapor, is needed. A table of calculated values is presented in the PDF. For the lower bound ultimate vacuum of 10^-8 Torr, the maximum allowable gas load of the system during pumpdown is 1.704 x 10^-7 Torr-L/S. For the upper bound vacuum level of 10^-2 Torr, now in transitional flow, the maximum allowable gas load is 1.191 x 10^-1 Torr-L/s.
3.) Total Gas Load
Now that the bounds have been established, the total gas load of the system can be calculated. The total gas load of the system can be found as the sum of the total gas loads due to the volume of the system, outgassing, diffusion, permeation, backstreaming, and the process gas flow. For pumpdown, volume can essentially be ignored since it will already be mostly pumped out from roughing. Assuming a perfectly sealed system, the gas load due to leaks can be eliminated for simplicity. Diffusion is not an issue for the metals present in the system at high vacuum levels under ultra-high and extreme vacuum levels, so this term can be ignored as well. Since a well-designed, optically opaque water cooled baffle will be employed, backstreaming can be ignored. Because this is pumpdown to high vacuum, no process gases will be introduced, so this gas load is also ignored. This leaves the gas loads due to outgassing and permeation.
To find the total outgassing load due to outgassing and permeation, the system is broken down into each component first, like when molecular and transitional flows are calculated. Then, the load due to outgassing for every material in the component is calculated, based on outgassing rates for the material and the entire surface area exposed to the vacuum. Permeation, which in this case is only due to Viton gaskets, is also calculated by multiplying the permeation constant to the total length of Viton. These numbers are summed together for the total gas load of the part, where all loads from all parts are then summed to find the total gas load of the system during pumping.
As something to note, this is where CAD becomes crucial. By having each part modeled out, it becomes incredibly easy to find the total surface area for each part, and the total lengths for each gasket. For the gaskets, both the length and the surface area must be calculated to find both the gas load due to outgassing as well as permeation. A worst case number was found by using the total surface area of the o-ring as opposed to only the surface exposed to vacuum. Outgassing constants vary between materials, as well as pumpdown times and temperatures. Therefore, the total gas loads where calculated for three different pumpdown scenarios: unbaked and pumped for 1 hour, unbaked and pumped for greater than 24 hours, and baked and pumped for greater than 24 hours. Baking temperature of the system is limited to about 150C due to the Viton gaskets and high vacuum transducers used. This calculation represents possibly the most tedious and exhausting due to an exceptional amount of variables to consider – all materials, all surface areas, as well as different pumpdown scenarios are factored in for the whole system as best as reasonably measurable and for practical purposes. Based on all of these measurements and calculations for the system, the total gas load of the system for pumpdown was found for the following three conditions:
Unbaked, Pumped 1hr
Q(total) = 2.903 x 10^-5 Torr-L/s
Unbaked, Pumped >24hr
Q(total) = 1.428 x 10^-5 Torr-L/s
Baked, Pumped >24hr
Q(total) = 9.589 x 10^-6 Torr-L/s
These relatively high loads are due to the Viton gaskets present in the system. These numbers in reality should be less due to the over-estimation of gas load on the system for the o-rings. From these numbers, the maximum achievable vacuum during pumpdown can finally be calculated.
4.) Maximum Achievable Vacuum During Pumpdown
Applying the equation S=q/P, where S is the effective speed for water vapor at the proper flow regime, q is the total gas load of the system during pumpdown, due to outgassing and permeation, and P is the ultimate pressure. Solving for P, using the effective speed for water vapor in molecular flow of 17.043 L/s, the following numbers are attained:
Unbaked, Pumped 1hr
P = 1.703 x 10^-6 Torr
Unbaked, Pumped >24hr
P = 8.379 x 10^-7 Torr-L/s
Baked, Pumped >24hr
P = 5.626 x 10^-7 Torr-L/s
Therefore, within reasonable confidence given simplified and worst case estimates, this system should be capable of reaching an ultimate vacuum level in the mid 10^-7 Torr pressure level, assuming the system is properly sealed, baked, outgassed, and pumped.
5.) Critical Factor Determination for Feasibility of Pumping System
A final design rule must be calculated for the system. For a high vacuum system, there is a critical pumping speed at which the system can be reasonably pumped down within a reasonable amount of time and effort, without the need to use cryopumping. This critical pumping speed factor is found by dividing the speed of the system by the total surface area of the high vacuum system. This number should be greater than or equal to 0.01 L/s/cm^2. For this example, it is calculated for two different scenarios, assuming water vapor for pumpdown – a simplified surface area model where only the total internal area of all the walls are found, and a over-estimated worst case scenario where the total surface area of all the surface are added to the total surface area of all of the Viton gaskets, even if the gasket face itself is not directly exposed to the high vacuum chamber. As a result:
Critical Pumping Speed for Internal Area Only = 0.020 L/s/cm^2
Critical Pumping Speed for All Possible Exposed Areas = 0.015 L/s/cm^2.
Therefore, the critical pumping speed of the system is valid for pumpdown.
Conclusion
Now that the total gas load during pumpdown, as well as the ultimate vacuum has been calculated for a variety of pumpdown conditions, the last steps are to find pumpdown times and the total allowable gas load for each gas over the expected range of vacuum for various processes. This step has been the most exhaustive of the process, employing the use of not only a wide range of constants for various materials and pumping conditions, but meticulous measurements and modeling in CAD, and factoring in all reasonably associated variables to give a good approximation of what to expect for the current system behavior. Based on the general principles and knowledge of high vacuum systems, the ultimate vacuum level approximations for this system are consistent with what one would expect in literature and practice.